包括无约束优化问题、带等式约束和不等式约束的凸优化问题的求解
无约束优化问题
无约束优化问题:
$$ \text { minimize } f_0(x) $$
对于凸问题而言,只有一个条件
$$ \nabla f (x^{\star}) = 0 $$
强凸性
存在一个大于0的$m$,使得
$$\forall x \in C, \nabla ^2 f(x) \geq mI$$ $$ f(y) = f(x) + \nabla f(x)^T (y-x) + \frac{m}2||x-y||_2^2 \newline f(x) - p^{\star} \leq \frac{1}{2m} ||\nabla f(x)||_2^2 $$
强凸性的性质:任何梯度足够小的点都是近似最优解(结束条件)
下降法
通用的求解方法都是迭代的下降方法,所谓下降,也就是每次迭代,后一个值都比前一个值对应的目标函数值要低,所以是下降。对于前一个值$x^{k}$,寻找一个方向$d^k$和步长$\alpha^k$,下一个值就是$x^{k+1} = x^k + \alpha^k d^k $,初始点、搜索方向、迭代步长也称为迭代搜索法的三要素。
由于无约束条件,初始点满足以下两项即可: ① $x^0 \in dom f$ ② 下水平集是一个闭集
初始点确定之后,还需要选择下降方向、步长、终止条件等
线搜索
$$ x^{k+1} = x^k + \alpha^k d^k $$
$d^{k}$是搜索方向。
希望能在这个方向上有个最大的下降,也就是找到 $$ \alpha^k = \text{argmin}_{\alpha} f(x^k + \alpha^k d^k) $$ 但是实际上相当于每次下降都引入了一个新的优化问题,虽然效果好但是计算量很大。
带Backtracing的线搜索
算法:
- 令步长$t$为允许的最大步长
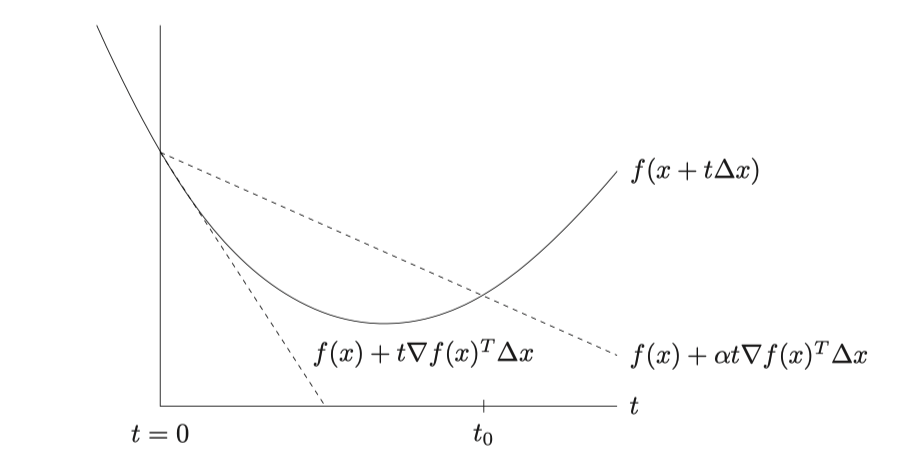
- 如果$f(x^k + t \Delta x) > f(x^k) + \alpha t \nabla f(x^k) \Delta x$(也就是说步长太大了,导致下降的一段比$\alpha * $斜率的长度还小,那就减少步长,右式后面是负数)
- 让$t = \beta t$
通常$\alpha $取0.5,$\beta$取一个0-1之间的数
这样就能找到一个比较合适的步长,而不需要非常高的计算量。
梯度下降法(最速下降法)
思想很简单,沿着梯度(梯度方向是函数值增加的方向)的反方向走,就可以使目标函数不断减少。
就像是下山,每次都沿着下降最快的方向走,最后一定能走到局部最低点(如果是凸函数就是全局最低点)
至于搜索步长,则选择这个一维方向搜索的最佳步长,因此,最速下降法的两个相邻迭代点的函数梯度相互垂直
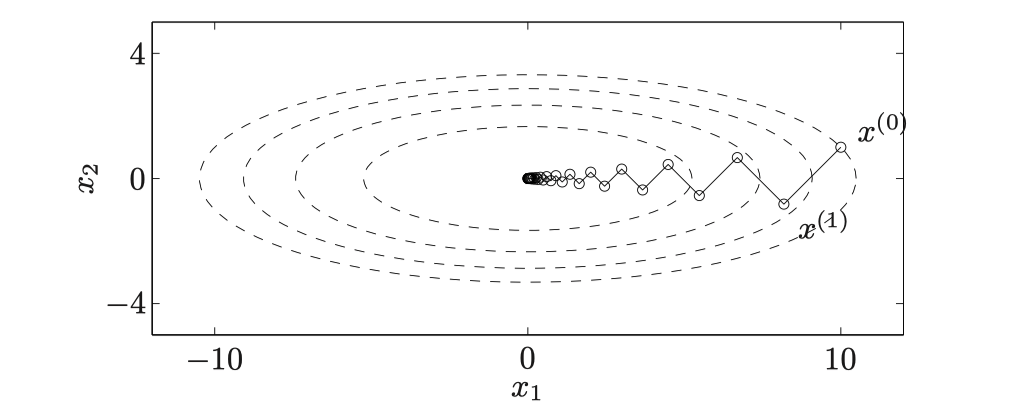
优点是可以沿着最快的方向,缺点是关注不到全局的情况,不关注下一个点的情况。
梯度下降法步骤: 输入:目标函数,目标函数梯度 输出:极小点
- 初始化$x^0$
- 计算搜索方向$d^k = - \nabla f(x^{k})$
- 如果小于$\epsilon$就停止迭代,否则就沿着$d^k$进行一维搜索,求最佳步长$\lambda^k$: $$ f(x^k + \lambda^k d^k) = \min_{\lambda \geq 0} f(x^k + \lambda d^k) $$
- 令$x^{k+1} = x^k + \lambda^k d^k$,转步骤2
选择最优步长的计算代价比较高
用最速下降法求目标函数$f(x) = x_1^2 + 25x_2^2$在$[2,2]^T$处的最速下降方向和步长 解:取初始点$x^0 = [2,2]^T$ 初始点函数值和梯度分别为: $f(x^0) = 104$ $\nabla f(x^0) = [4, 100]^T$ 沿负梯度方向进行一维搜索:
$$x^1 = x^0 - \alpha^0 \nabla f(x^0) = [2-4\alpha^0, 2-100\alpha^0]^T$$
$\alpha^0$需要满足极值条件:
$$ \min_\alpha f(x^1) = \min_\alpha ((2-4\alpha)^2 + 25 (2-100\alpha)^2) $$
解得$\alpha_0 = 0.02003$
牛顿法
牛顿法(Newton's Method)是一个非常有效的非线性方差的求根方法,主要用于求方程的根和求解最优化问题。
利用牛顿法,可以迭代求解非常复杂的方程的根: $$ f(x) = f(x_0) + f'(x_0)(x-x_0) + O((x-x_0)^2)\newline $$ 忽略截断误差后令$f(x)=0$可解得: $$ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} $$ $x_1$一定比$x_0$更接近真实根,从而不断迭代
对于最优化问题的求解
牛顿法的推导
当前点$v$,下降向量$v$,下降后的值为:
$$ f(x+v) \approx f(x)+\nabla f(x)^{T} v+\frac{1}2 v^{T} \nabla^2 f(x) v $$
要使该值最小,且$x$已经固定,关于$v$求偏导:
$$ \nabla f(x)+\nabla^2 f(x) v=0 $$
得到:
$$ \Delta x_{nt} = v=-\nabla^2 f(x)^{-1} \nabla f(x) $$
从而推出牛顿法的迭代公式: $$ x^{k+1} = x^k + \Delta x_{nt} = x^k -\nabla^2 f(x)^{-1} \nabla f(x) $$
$\nabla^2 f(x)$是$f(x)$的Hessian矩阵
一维时有: $$ x^{k+1} = x^k - \frac{f'(x^k)}{f''(x^k)} $$
多元函数保留到二次项得到: $$ f(x) = f(x^k) + \nabla f(x^k)^T(x-x^k) + \frac{1}2 (x-x^k)^T \nabla^2 f(x^k)(x-x^k) $$ 其中$\nabla^2 f(x^k)$是点$x^k$处的海森矩阵 通过求导得到平稳点,解得 $$ x^{k+1} = x^k - [\nabla^2 f(x^k)]^{-1}\nabla f(x^k) $$
求解无约束优化问题
牛顿法用二阶海森矩阵的逆矩阵求解,收敛更快但是每次迭代的计算时间更长
求目标函数$f(x) = x_1^2 + 25x_2^2$在$[2,2]^T$处的牛顿方向
解:初始点梯度$\nabla f(x_0) = [2x_1\ 50x_2]^T = [4\ 100]^T$ $$ \nabla^2 f(x^0)=\left[\begin{array}{cc} 2 & 0 \newline 0 & 50 \end{array}\right] $$ $$ [\nabla^2 f(x^0)]^{-1}=\left[\begin{array}{cc} \frac{1}2 & 0 \newline 0 & \frac{1}{50} \end{array}\right] $$ 牛顿方向为 $$- [\nabla^2 f(x^k)]^{-1}\nabla f(x^k) = -\left[\begin{array}{cc} \frac{1}2 & 0 \newline 0 & \frac{1}{50} \end{array}\right] \left[\begin{array}{cc} 4 \newline 100 \end{array}\right] = \left[\begin{array}{cc} -2 \newline -2 \end{array}\right]$$
阻尼牛顿法
增加了沿牛顿方向的一维搜索,步长$\lambda_k$由一维搜索得到,每次迭代必然下降,不过会增大计算量
共轭梯度法
$A$是对称正定矩阵,如果有两个方向$d^i, d^j$满足$(d^{i})^T A d^j$,则称这组方向是$A$共轭的 (如果$A$是单位阵,则称两个方向正交)
依次沿着$d^i$和$d^j$进行一维搜索,经过两次迭代必定到达极小点
拟牛顿法
计算海森矩阵的逆比较复杂,通过一个$n$阶矩阵来近似代替,就是拟牛顿法的思想。
$p^k \approx \nabla^2 f(x^{k+1})^{-1}q^k$
带等式约束的凸优化问题
对于带等式约束的凸优化问题: $$ \begin{array}{ll} \text{ minimize } & f_0(x) \newline \text { subject to } & Ax = b \end{array} $$
带等式约束的凸优化问题通常可以采用下面三种方法进行求解:
- 消除等式约束
- 利用无约束优化方法求解对偶问题
- 拓展的Newton法
消除等式约束
等式约束为$Ax = b$
满足此约束的$x$可以写为$Fy + \hat{x}$的形式,最后变成了: $$ \text{ minimize } f_0(Fy + \hat{x}) $$
的无约束优化问题,解得最优解$y^{\star}$之后,就可以通过$x^{\star} = Fy^{\star} + \hat{x}$计算出$x^{\star}$
比如: $$ \begin{array}{ll} \text{ minimize } & f_{1}\left(x_{1}\right)+f_2\left(x_2\right)+\cdots+f_{n}\left(x_{n}\right) \newline \text { subject to } & x_{1}+x_2+\cdots+x_{n}=b \end{array} $$
可以通过 $x_n = b - x_1 - ... - x_{n-1}$ 令$\hat{x} = b e_n$, $F = \left[\begin{array}{c} I \newline -\mathbf{1}^{T} \end{array}\right] \in \mathbf{R}^{n \times(n-1)}$
问题变为:
$$ \text{minimize}\ f_{1}\left(x_{1}\right)+\cdots+f_{n-1}\left(x_{n-1}\right)+f_{n}\left(b-x_{1}-\cdots-x_{n-1}\right) $$
通过对偶的方式转换为无约束问题
也就是前面对偶的解法
$$g(v) = -b^T + \inf_x (f(x) + v^T Ax) = -b^Tv - f^{\star} (-A^T v)$$
其中$f^{\star}$是$f$的共轭,通过解对偶问题:
$$ \text{maximize}\ -b^T v - f^{\star} (-A^T v) $$
就可以使用无约束的优化方法来求解
通过KKT条件可以知道,最优解$x^{\star}$满足: $$ Ax^{\star} = b \newline \nabla f(x^{\star}) + A^T v^{\star} = 0 $$
拓展Newton法
牛顿法除了求解无约束优化问题外,也可以用于求解带等式约束的凸优化问题。
在此之前先讨论等式约束凸二次规划问题: $$ \begin{array}{ll} \text{ minimize } & f(x)=(1 / 2) x^{T} P x+q^{T} x+r \newline \text { subject to } & A x=b, \end{array} $$
其KKT条件是: $Ax^{\star} = b, Px^{\star} + q + A^T v^{\star} = 0$
可以写成矩阵形式: $$ \left[\begin{array}{cc} P & A^{T} \newline A & 0 \end{array}\right]\left[\begin{array}{l} x^{\star} \newline \nu^{\star} \end{array}\right]=\left[\begin{array}{c} -q \newline b \end{array}\right] $$
也称为KKT矩阵
这里有等式约束的拓展牛顿法与无约束的牛顿法不同的是需要保证牛顿方向$\Delta x_{nt}$是可行的,也就是:$A \Delta x_{nt} = 0$
等式约束问题: $$ \begin{array}{ll} \text{ minimize } & f(x) \newline \text { subject to } & Ax = b \end{array} $$
在可行点$x$处的牛顿方向$\Delta x_{nt}$,目标函数转换为二阶近似: $$ \begin{array}{ll} \text{ minimize } & f(x+v) = f(x) + \nabla f(x)^T v + (1/2) v^T \nabla^2 f(x) v\newline \text { subject to } & A(x+v) = b \end{array} $$
这里的KKT矩阵是:
$$ \left[\begin{array}{cc} \nabla^2 f(x) & A^{T} \newline A & 0 \end{array}\right]\left[\begin{array}{c} \Delta x_{\mathrm{nt}} \newline w \end{array}\right]=\left[\begin{array}{c} -\nabla f(x) \newline 0 \end{array}\right] $$
等式约束的牛顿减量定义为: $$ \lambda(x)=\left(\Delta x_{\mathrm{nt}}^{T} \nabla^2 f(x) \Delta x_{\mathrm{nt}}\right)^{1 / 2} $$
等式约束优化问题的牛顿法:
- 计算牛顿方向$\Delta x_{nt}$和牛顿减量$\lambda(x)$
- 如果$\frac{\lambda^2}2 \leq \epsilon$就退出
- 直线搜索确定步长
- $x = x+t \Delta x_{nt}$
带不等式约束的凸优化问题
带不等式约束的凸优化问题,通过障碍法将不等式约束加入目标函数,从而把问题转换为带等式约束的优化问题,从而可以使用上一节的方法进行求解。
对于凸优化问题: $$ \begin{array}{ll} \text{ minimize } & f_0(x) \newline \text { subject to } & f_{i}(x) \leq 0, \quad i=1, \ldots, m \newline & Ax = b \end{array} $$
对数障碍法:
将其转换为等式约束问题: $$ \begin{array}{ll} \text{ minimize } & f_0(x) + \sum_{i=0}^m I_-(f_i(x)) \newline \text { subject to } & Ax = b \end{array} $$
其中 $$I_- (x) = \left \{ \begin{array}{ll} 0 & \text{if } x \leq 0 \newline \infty & \text{otherwise} \end{array} \right . $$
也就是说不满足不等式约束的话,就让目标函数无限大,否则就没影响。 但是这个函数不可导,所以采用一个对数函数来近似:
$$I_- (x) = -\frac{1}{t} log(-x)$$
定义$\phi(x) = - \sum_{i=1}^m \log(-f_i(x))$为对数障碍函数,其梯度为: $$ \nabla \phi(x) = \sum_{i=1}^m \frac{1}{-f_i(x)} \nabla f_i(x) $$ 其Hessian矩阵为: $$ \nabla^2 \phi(x)=\sum_{i=1}^{m} \frac{1}{-f_{i}(x)} \nabla^2 f_{i}(x)+\sum_{i=1}^{m} \frac{1}{f_{i}(x)^2} \nabla f_{i}(x) \nabla f_{i}(x)^{T} $$
例题
给定函数$f(x)=(6+x_1+x_2)^2+(2-3x_1-3x_2-x_1x_2)^2$,求在点$(\hat{X}=(-4,6)^T)$处的牛顿方向$d$
$$ \nabla^T f(x) = \left [ \begin{array}{cc} 2(6 + x_1 + x_2) + 2(2-3x_1 - 3x_2 - x_1 x_2 )(-3-x_2) \newline 2(6 + x_1 + x_2) + 2(2-3x_1 - 3x_2 - x_1 x_2 )(-3-x_2) \end{array} \right ] = \left [ \begin{array}{cc} -344 \newline 56 \end{array} \right ] $$
$$ \nabla^2 f(x) = \left [ \begin{array}{cc} 2 + 2(3+x_2)^2 & 2 + 2(3+x_1)(3+x_2) -2 (2-3x_1 - 3x_2 -x_1 x_2)\newline 2 + 2(3+x_2)(3+x_1) -2 (2-3x_1 - 3x_2 -x_1 x_2) & 2 + 2(3+x_1)^2 \end{array} \right ] = \left [ \begin{array}{cc} 164 & -56 \newline -56 & 4 \end{array} \right ] $$
$$ [\nabla^2 f(x)]^{-1} = -\frac{1}{2480} \left [ \begin{array}{cc} 4 & 56 \newline 56 & 164 \end{array} \right ] $$
$$ \begin{array}{ll} \triangle x_{nt} &= -(\nabla^2 f(x))^{-1} \nabla f^T(x)\newline &=\frac{1}{2480} \left [ \begin{array}{cc} 4 & 56 \newline 56 & 164 \end{array} \right ] \left [ \begin{array}{cc} -344 \newline 56 \end{array} \right ] = \left [ \begin{array}{cc} -0.709677 \newline 4.064516 \end{array} \right ] \end{array} $$
牛顿方向为$d = \left [ \begin{array}{cc} -0.709677 \newline 4.064516 \end{array} \right ]$
利用牛顿法求解$\min f(x) = (x_1 - 4)^2 + x_2^4$并给出迭代过程,初始点为$[0\ 1]^T$
第一次迭代: $$ \nabla^T f(x^0) = \left [ \begin{array}{cc} 2(x_1 -4)\newline 4x_2^3 \end{array} \right ] = \left [ \begin{array}{cc} -8 \newline 4 \end{array} \right ] $$
$$ \nabla^2 f(x^0) = \left [ \begin{array}{cc} 2 & 0\newline 0 & 12x_2^2 \end{array} \right ] = \left [ \begin{array}{cc} 2 & 0\newline 0 & 12 \end{array} \right ] $$
$$ [\nabla^2 f(x^0)]^{-1} = \left [ \begin{array}{cc} \frac{1}2 & 0 \newline 0 & \frac{1}{12} \end{array} \right ] $$
$$ \begin{array}{ll} x^1 &= x^0 + \triangle x^0_{nt} = x^0 -(\nabla^2 f(x^0))^{-1} \nabla f^T(x^0)\newline &=\left [ \begin{array}{cc} 0 \newline 1 \end{array} \right ] - \left [ \begin{array}{cc} \frac{1}2 & 0 \newline 0 & \frac{1}{12} \end{array} \right ] \left [ \begin{array}{cc} -8 \newline 4 \end{array} \right ] = \left [ \begin{array}{cc} 4 \newline \frac2{3} \end{array} \right ] \end{array} $$
第二次迭代:
$$ \nabla^T f(x^1) = \left [ \begin{array}{cc} 2(x_1 -4)\newline 4x_2^3 \end{array} \right ] = \left [ \begin{array}{cc} 0 \newline \frac{32}{27} \end{array} \right ] $$
$$ \nabla^2 f(x^1) = \left [ \begin{array}{cc} 2 & 0\newline 0 & 12x_2^2 \end{array} \right ] = \left [ \begin{array}{cc} 2 & 0\newline 0 & \frac{16}{3} \end{array} \right ] $$
$$ [\nabla^2 f(x^1)]^{-1} = \left [ \begin{array}{cc} \frac{1}2 & 0 \newline 0 & \frac{3}{16} \end{array} \right ] $$
$$ \begin{array}{ll} x^2 &= x^1 + \triangle x^1_{nt} = x^1 -(\nabla^2 f(x^1))^{-1} \nabla f^T(x^1)\newline &=\left [ \begin{array}{cc} 4 \newline \frac2{3} \end{array} \right ] - \left [ \begin{array}{cc} \frac{1}2 & 0 \newline 0 & \frac{3}{16} \end{array} \right ] \left [ \begin{array}{cc} 0 \newline \frac{32}{27} \end{array} \right ] = \left [ \begin{array}{cc} 4 \newline \frac{4}{9} \end{array} \right ] \end{array} $$
第三次迭代: 同理 $$ \begin{array}{ll} x^3 &= x^2 + \triangle x^2_{nt} = x^2 -(\nabla^2 f(x^2))^{-1} \nabla f^T(x^2)\newline &=\left [ \begin{array}{cc} 4 \newline \frac{4}{9} \end{array} \right ] - \left [ \begin{array}{cc} \frac{1}2 & 0 \newline 0 & \frac{27}{64} \end{array} \right ] \left [ \begin{array}{cc} 0 \newline \frac{256}{729} \end{array} \right ] = \left [ \begin{array}{cc} 4 \newline \frac{8}{27} \end{array} \right ] \end{array} $$
之后同理