基本形式
一般的优化问题的形式: $$ \begin{array}{ll} \text { minimize } & f_0(x) \newline \text { subject to } & f_{i}(x) \leq 0, \quad i=1, \ldots, m \newline & h_{i}(x)=0, \quad i=1, \ldots, p \end{array} $$
其中$x$是优化变量,$f_0(x)$是目标函数 ,$f_i(x)\leq 0$是不等式约束,$h_i(x) = 0$是等式约束。如果$m=p=0$,就是无约束问题。
定义域为 $$ \mathcal{D}=\bigcap_{i=0}^{m} \operatorname{dom} f_{i} \cap \bigcap_{i=1}^{p} \operatorname{dom} h_{i} $$
如果满足目标函数是凸函数,不等式约束也是凸函数,等式约束函数是仿射函数。就是凸优化问题。 $$ \begin{array}{ll} \text{ minimize } & f_0(x) \newline \text { subject to } & f_{i}(x) \leq 0, \quad i=1, \ldots, m \newline & a_{i}^{T} x=b_{i}, \quad i=1, \ldots, p \end{array} $$
定义域为: $$ \mathcal{D}=\bigcap_{i=0}^{m} \operatorname{dom} f_{i} $$
可行解集(feasible set),即在目标函数的定义域中的满足所有约束的解集: $$ X_f = \{x | x满足所有约束\} $$
问题的最优值(optimal value),如果可行解集不是空集,总能在可行解集中找到一个值,使目标函数最小,这个解就是最优解: $$p^\star = inf\{f_0(x)|x \in X_f\}$$
这里inf是下确界的意思,和min类似但是不完全相同。有可能有下确界但是无限趋近取不到,也就是有inf没有min。
凸优化问题的最重要性质(为什么要研究凸优化,为什么要转换为凸优化问题):局部最优 = 全局最优
证明凸优化问题的局部最优=全局最优: $$\newline$$ 一句话说明就是反证法假设在局部最优之外还能找到一个全局最优,根据凸函数的性质,就可以在局部最优的领域内找到更低的点,从而与局部最优矛盾,具体过程如下: $$\newline$$ 反证法:假设局部最优解x不是全局最优解y。 $$\newline$$ 因为局部最优,所以一定能找到一个正数$R$,使得在$R$的范围内,$f_0(x)$是最小的,即: $$ \exists R > 0 , f_0(x) = inf { f_0(z), ||x-z||_2\leq R }$$ 假设全局最优解是$y$ $$y \neq x, f_0(y) < f_0(x), ||y-x||_2 > R$$ 由于是凸函数,在$x、y$中间的一点$ z= (1-\theta) x + \theta y$,有: $$f_0(z) \leq (1-\theta)f_0(x) + \theta f_0(y)$$ 令$\theta = \frac{R}{2||y-x||_2}$ 因为可行域是凸集,z一定是可行解。 计算得$||z-x||_2 = \frac{R}2$(实际上前面取$\theta$等于那个的目的就是为了让这里 z在x的邻域内) 因为在邻域内x一定最优,所以$f_0(z) > f_0(x)$。最优点y的$f_0(y) < f_0(x)$ 结合前面的式子,有$f_0(z) \leq (1-\theta)f_0(x) + \theta f_0(y) < f_0(z) $,矛盾了,找不到z,也就是说局部最优就是全局最优。
可微的目标函数的最优解x,当且仅当: $$\triangledown f_0(x)^T (y-x) \geq 0\ \ \ \text{for all feasible}\ y$$
用凸函数的一阶等价定义$f(y) \geq f(x) + \triangledown f^T(x) (y-x)$即可直接证明
等价问题
Box constraint
例: $$ \begin{array}{ll} \text { minimize } & f_0(x) \newline \text { subject to } & l_i \leq x \leq u_i, i = 1, ... ,n \end{array} $$
改写为标准形式为
$$ \begin{array}{ll} \text { minimize } & f_0(x) \newline \text { subject to } & l_i - x \leq 0, i = 1, ... ,n \newline & x - u_i \leq 0, i = 1, ... ,n \end{array} $$
函数等价变换
| $\psi_0$ | $R \to R$ | 单增 |
|---|---|---|
| $\psi_1, \dots \psi_m$ | $R \to R$ | $\psi_{i}(u) \leq 0 \Leftrightarrow u \leq 0$ |
| $ϱ_1,\dots ϱ_p$ | $R \to R$ | $ϱ_{i}(u) = 0 \Leftrightarrow u = 0$ |
变为: $$ \begin{array}{lll} \min & \psi_0\left(f_0(x)\right) & \newline \text { s.t. } & \psi_{i}\left(f_{i}(x)\right) \leq 0 & i=1, \ldots, m \newline & \varrho_{i}\left(h_{i}(x)\right)=0 & i=1, \ldots, p \end{array} $$
比如 $$ \min |A x-b|_2 \Leftrightarrow|A x-b|_2^2 $$
消除或引入等式约束
比如 $$ \begin{array}{ll} \text { minimize } & f_0(x) \newline \text { subject to } & f_i (x) \leq 0, i = 1, ... ,m \newline & Ax = b \end{array} $$
可以等价于: $$ \begin{array}{ll} \text { minimize } & f_0(Fz + x_0) \newline \text { subject to } & f_i (Fz + x_0) \leq 0, i = 1, ... ,m \end{array} $$
从而消除一个等式约束,也可以从下往上,增加一个等式约束
松弛变量
将不等号通过松弛变量变为等号 比如 $$ \begin{array}{ll} \text { minimize } & f_0(x) \newline \text { subject to } & a^T_i (x) \leq b, i = 1, ... ,m \newline \end{array} $$
可以等价于: $$ \begin{array}{ll} \text { minimize } & f_0(Fz + x_0) \newline \text { subject to } & a^T_i (x) + s_i = b, i = 1, ... ,m \newline & s_i \geq 0, i = 1, ... ,m \end{array} $$
如何把实际问题转换为标准凸优化问题形式
极大化一个凹目标函数,实际上就是凸优化问题
典型的凸优化问题
线性规划
目标函数、等式约束、不等式约束均为线性
$$ \begin{array}{ll} \text{ minimize } & c^{T} x+d \newline \text { subject to } & G x \preceq h \newline & A x=b \end{array} $$
至少有一个最优解在顶点上
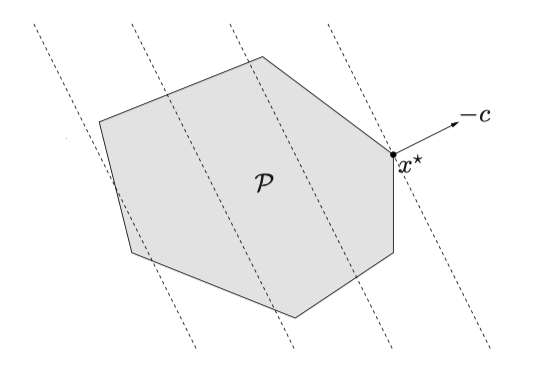
二次规划
目标是二次凸函数,约束函数均为线性
$$ \begin{array}{ll} \text{ minimize } & (1 / 2) x^{T} P x+q^{T} x+r \newline \text { subject to } & G x \preceq h \newline & A x=b \end{array} $$
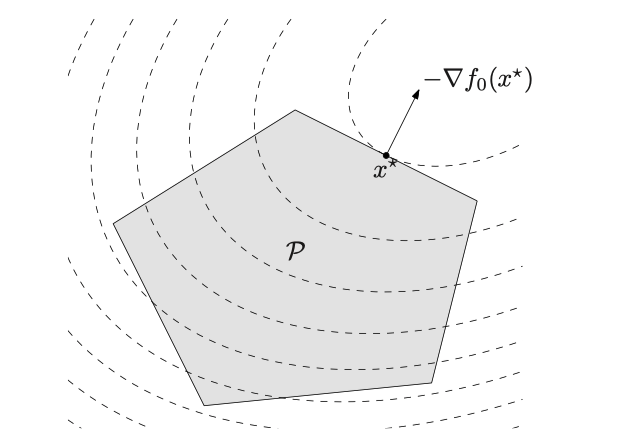
例题
考虑优化问题: $$ \begin{array}{ll} \text { minimize} & f_0\left(x_{1}, x_2\right) \newline \text { subject to } & 2 x_{1}+x_2 \geqslant 1 \newline & x_{1}+3 x_2 \geqslant 1 \newline & x_{1} \geqslant 0, \quad x_2 \geqslant 0 \end{array} $$ 对下面每个目标函数给出最优解和最优值
(a) 最优解$x^* = (\frac2{5}, \frac{1}{5})$ 最优值$f(x^*) = \frac{3}{5}$
(b) 目标函数没有下界
(c) 最优解为$x^* = (0, x_2), x_2 \geq 1$ 最优值$f(x^*) = 0$
(d) 最优解$x^* = (\frac{1}{3}, \frac{1}{3})$ 最优值$f(x^*) = \frac{1}{3}$
(e) 最优解$x^* = (\frac{1}2, \frac{1}{6})$ 最优值$f(x^*) = \frac{1}2$
考虑线性规划 $$ \begin{array}{ll} \text { minimize } & c^{T} A^{-1} y \newline \text { subject to } & y \preceq b \end{array} $$ A是方阵且不奇异,说明其最优值由: $$ p^{\star}= \begin{cases}c^{T} A^{-1} b & A^{-T} c \preceq 0 \newline -\infty & \text { 其他情况 }\end{cases} $$ 给出
令$Ax = y$,则有$x = A^{-1}y$
$$ \begin{array}{ll} \text { minimize } & c^{T} A^{-1} y \newline \text { subject to } & y \preceq b \end{array} $$
如果$A^{-T} c \preceq 0$,最优解即为$y=b$,否则y取$- \infty$,函数无下界。
网络流问题,网络总费用为$C = \sum_{1,j=1}^n c_{ij}x_{ij}$,每个边流量$x_{ij}$同时收到下界$l_{ij}$和上界$u_{ij}$的约束,流出和流入的流量守恒。建模成一个线性规划问题
目标函数为: $$ \text{minimize}\ C = \sum_{1,j=1}^n c_{ij}x_{ij} $$ 约束有: $$ \left \{ \begin{array}{ll} l_{ij} \leq x_{ij} \leq u_{ij} \newline b_i + \sum_{j=1}^n x_{ij} - \sum_{j=1}^n x_{ji} = 0 \end{array} \right . $$
线性规划即为: $$ \begin{array}{ll} \text { minimize } & C = \sum_{1,j=1}^n c_{ij}x_{ij} \newline \text { subject to } & l_{ij} \leq x_{ij} \leq u_{ij} \newline & b_i + \sum_{j=1}^n x_{ij} - \sum_{j=1}^n x_{ji} = 0, i = 1, ... n \end{array} $$
Gauss广播信道的最优功率与带宽配置,建模为凸优化问题
目标函数为: $$ \sum_{i=1}^{n} u_{i}\left(R_{i}\right) = \sum_{i=1}^{n} u_{i}(\alpha_{i} W_{i} \log \left(1+\beta_{i} P_{i} / W_{i}\right)) $$
约束有: $$ \left \{ \begin{array}{ll} \sum P_{i=1}^n = P_{tol}\newline \sum W_{i=1}^n = W_{tol}\newline \end{array} \right . $$
R的Hassain矩阵为$$ \nabla^2 R_{i}=\frac{-\alpha_{i} \beta_{i}^2}{W_{i}\left(1+\beta_{i} P_{i} / W_{i}\right)^2}\left[\begin{array}{c} 1 \newline -P_{i} \end{array}\right]\left[\begin{array}{c} 1 \newline -P_{i} \end{array}\right]^{T}$$ 是负定的,说明$R_i$是凹的。总效用是凹函数的和,也是凹函数。