凸函数的定义
定义一(基本定义)
函数$f: R^n \to R$是凸函数,当且仅当:
- $f$的定义域是凸集
- $\forall x_1, x_2 \in dom(f), \forall \theta \in [0,1]$ $f(\theta x_1+(1-\theta)x_2) \leq \theta f(x_1) + (1-\theta)f(x_2)$
该式也叫Jenson不等式: $$f(\theta x + (1-\theta) y) \leq \theta f(x) + (1-\theta)f(y)$$
拓展,对于任意随机变量z,有 $$f(Ez) \leq Ef(z)$$
通俗来讲,就是函数上任取两点,它们之间的连线都在函数的上面
如果2的$\leq$换成$<$就是严格凸函数
定义二(降至一维)
函数$f: R^n \to R$是凸函数,当且仅当:
- $f$的定义域是凸集
- $\forall x \in dom\ f, \forall v, g(t) = f(x+tv)$为凸函数,$dom\ g \in dom\ f$
相当于从高维降到一维,可以通过证明一维的函数$g(t)$来反证原函数$f(x)$,当然这个定义用的不多
定义三(凸函数的一阶条件)
若$f: R^n \to R$一阶可微,则它是凸函数,当且仅当:
- $f$的定义域是凸集
- $\forall x, y \in dom(f), f(y) \geq f(x) + \triangledown f(x)^T (y-x)$
通俗来讲,就是任何一点的切线,切线上的任何一点都小于等于函数
证明定义三:
充分性:首先因为是凸函数,定义域为凸集。代入$y \to x+$即可 必要性:构造$z = \theta x + (1-\theta)y$,然后代入f(x)和f(y)的一阶不等式到$\theta f(x) + (1-\theta) f(y)$中即可得到结果。
定义四(凸函数的二阶条件)
实际上用的最多,前提是二阶可微
若$f: R^n \to R$二阶可微,则它是凸函数,当且仅当:
- $f$的定义域是凸集
- $\forall x \in dom(f), \triangledown f^2(x) \geq 0$,即$f$的Hessian矩阵半正定(特征值均$\geq 0$)
如何判断矩阵的正定或负定? $$\newline$$ 方法一、正定矩阵的顺序主子式均为正 $$\newline$$ 例: $$ \begin{array}{ccc} \end{array} \left | \begin{array}{ccc} 6 & -3 & 1 \newline -3 & 2 & 0 \newline 1 & 0 & 4 \newline \end{array} \right | $$ 三个顺序主子式依次为: $$ \left | \begin{array}{ccc} 6 \newline \end{array} \right | = 6 > 0 $$ $$ \left | \begin{array}{ccc} 6 & -3 \newline -3 & 2 \newline \end{array} \right | = 3 > 0 $$ $$ \left | \begin{array}{ccc} 6 & -3 & 1 \newline -3 & 2 & 0 \newline 1 & 0 & 4 \newline \end{array} \right | = 10 > 0 $$ 所以为正定矩阵 $$\newline$$ 方法二:$x^T H x \geq 0$ (一般用来求二阶的情况,高阶不好求。) $$\newline$$ 例: $$ H = \begin{array}{ccc} \end{array} \left [ \begin{array}{ccc} 3 & 2 \newline 2 & 1 \newline \end{array} \right ] $$ 对于任意$x$,构造 $$ x^T \begin{array}{ccc} \end{array} \left [ \begin{array}{ccc} 3 & 1 \newline 1 & 1 \newline \end{array} \right ] x = 3x_1^2 + 2x_1 x_2 + x_2^2 = 2x_1^2 + (x_1+x_2)^2 \geq 0 $$ 所以是半正定的
注意,使用该方法时需要定义域是凸集,且二阶可微,比如$f(x)=\frac{1}{x^2}$,即使二阶导数$\geq0$,因为在0不连续,定义域不是凸集,所以不是凸函数。
第一个要判断的就是定义域是否为凸集。然后看定义域内是否可导,比如某分段函数的某点是尖不可导,当然不能说一定凸/非凸,只是说不能用这个定义判断,要用基本定义来求。
如果取$>$,那么是严格凸的,但是并不是凸函数都能取$>$,比如$x^4$在0处的二阶导就是0
凸函数拓展
如果$f(x)$是凸函数,那么凸函数的拓展
$$ \bar{f}(x)= \begin{cases}f(x) & x \in \operatorname{dom}(f) \newline \infty & x \notin \operatorname{dom}(f)\end{cases} $$
也是凸函数,比较直观
常见的凸函数
仿射函数
$ f(x) = Ax + b$
$\nabla^{2} f(x) = 0$ 仿射函数既是凸函数,又是凹函数
指数函数
$f(x) = e^{ax}$
$\nabla^{2} f(x) = a^2 e^{ax} > 0$
幂函数
$f(x) = x^a$
分情况讨论
$$\nabla^{2} f(x)=a(a-1) x^{a-2}=\left\{\begin{array}{ll}\geq 0 & a \geq 1, a \leq 0 & 凸\newline \leq 0 & a \in[0,1]& 凹\end{array}\right.$$
绝对值幂函数
$f(x) = |x|^p$
$$ f^{\prime \prime}(x)= \begin{cases}p(p-1) x^{p-2} & x \geq 0 \newline -p(p-1)(-x)^{p-2} & x<0\end{cases} $$
情况比较复杂,需要对$p$分类讨论。
范数
$R^n$空间的范数$P(x)$
有如下性质: ① $P(ax) = |a|P(x)$ ② $P(x+y) \leq P(x) + P(y)$ ③ $P(x) = 0 \Leftrightarrow x = 0$
范数是凸函数,按照定义用性质②即可证明(零范数除外,零范数不满足①)
极大值函数
$f(x) = max\{x_1, x_2, ...x_n\}$
极大值函数是凸函数,所以会有极小极大问题,即极小化一个极大值函数
共轭函数
保凸运算
非负加权和
$f_1, ..., f_m$为凸,$\omega_i \geq 0$,则$f = \sum_{i=1}^{m} \omega_i f_i$为凸
仿射映射
$f: R^n \to R$为凸,则$g(x) = f(Ax+b)$为凸
凸函数的逐点最大
$f_1, f_2$为凸,则$f = \max{{f_1(x), f_2(x)}}$为凸
可以用定义一证明,可以推广到无数个
比如分段线性函数就是凸函数
复合函数
$f(x) = h(g(x))$
$ f^{\prime \prime}(x)=h^{\prime \prime}(g(x)) g^{\prime 2}(x)+h^{\prime}(g(x)) g^{\prime \prime}(x) $
然后分情况讨论
拟凸函数与拟凹函数
$\alpha$-下水平集:$$ C_{\alpha}={x \in \operatorname{dom} f \mid f(x) \leq \alpha} $$
指的是定义域是凸集!
如果作一条水平线,交点数>2,必然不是拟凸
考虑函数的$\alpha-$下水平集,凸函数的所有$\alpha$-下水平集是凸集,但是$\alpha$-下水平集是凸集的函数不一定是凸函数
拟凸有时候也称为单模态函数,如下图左图为拟凸函数,右图则不是拟凸函数
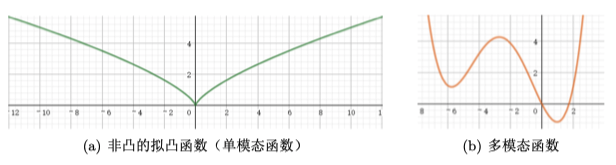
定义函数$f: R^n \to n$是拟凸函数,如果其定义域和所有$\alpha$-下水平集都是凸集: $$S_\alpha = { x\in dom f | f(x) \leq \alpha }$$
对于拟凸函数$f$,有:(Jensen不等式) $$f(\theta x + (1-\theta)y) \leq max{ f(x), f(y)}, 0 \leq \theta \leq 1$$
凸函数一定是拟凸函数,但是拟凸函数不一定是凸函数。
拟凹函数同理,即为上水平集均为凸的函数。
例题
假设$f :R \to R$是凸函数,$$a,b \in \textbf{dom} f, a < b$$ (a)证明对于任意$x\in [a,b]$,下式成立: $$ f(x) \leq \frac{b-x}{b-a} f(a)+\frac{x-a}{b-a} f(b) $$ (b)证明对于任意$x \in (a,b)$,下式成立(并画一个草图说明): $$ \frac{f(x)-f(a)}{x-a} \leq \frac{f(b)-f(a)}{b-a}\leq \frac{f(b)-f(x)}{b-x} $$ (c)假设$f$可微,利用(b)的结论证明: $$ f'(a) \leq \frac{f(b)-f(a)}{b-a} \leq f'(b) $$ (d)假设$f$二次可微,利用(c)的结论证明$f''(a)\geq 0$和$f''(b)\geq 0$
(a) 由凸函数的定义可知,定义域上任意两点$x, y$,对任意$\theta \in [0,1]$有: $f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y)$
$a, b \in dom f, x\in[a,b]$ 取$\theta = \frac{b-x}{b-a} \in dom f$ 有$f(x) = f(\frac{b-x}{b-a}a + \frac{x-a}{b-a}b) \leq \frac{b-x}{b-a} f(a)+\frac{x-a}{b-a} f(b)$
(b) (a)中的式子左右两边都减去$f(a)$,即可得到$\frac{f(x)-f(a)}{x-a} \leq \frac{f(b)-f(a)}{b-a}$,左右两边都减去$f(b)$,即可得到$\frac{f(b)-f(a)}{b-a} \leq \frac{f(b)-f(x)}{b-x}$ 草图如下:
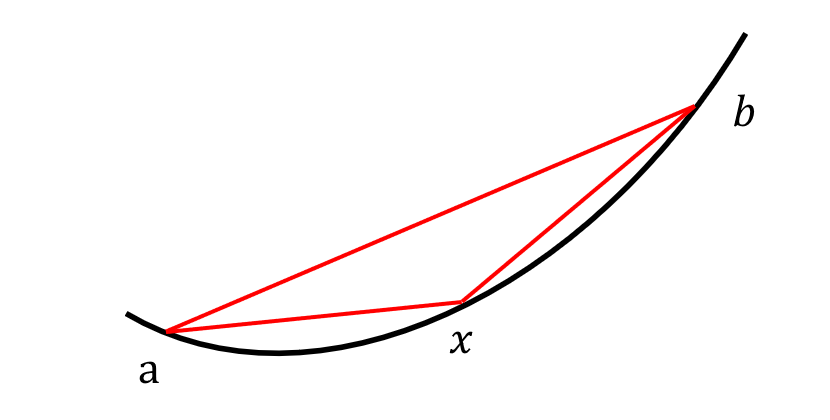
不等式描述了斜率:$\overline{ax} \leq \overline{ab} \leq \overline{xb}$
(c) 取$x \to a+$,代入(b)的前半部分即有$f'(a) = \lim_{x\to a+} \frac{f(x)-f(a)}{x-a} \leq \frac{f(b)-f(a)}{b-a}$,同理,取$x \to b-$,代入(b)的后半部分即有$\frac{f(b)-f(a)}{b-a} \leq \lim_{x\to b-} = f'(b)$
(d)
(c)的结果为: $f'(a) \leq \frac{f(b)-f(a)}{b-a} \leq f'(b)$
在此基础上令$b \to a+$ $f''(a) = \lim_{b\to a+} \frac{f'(b) - f'(a)}{b-a} \geq 0 $
同理可得$f''(b) \geq 0$
证明连续函数$f: R^n \to R$是凸函数的充要条件是,对于任意线段,函数在线段上的平均值不大于线段端点函数值的平均,也就是对于任意$x, y \in R^n$,下式成立: $$ \int_{0}^{1} f(x+\lambda(y-x)) d \lambda \leqslant \frac{f(x)+f(y)}{2} $$
先证明必要性,如果连续函数$f$是凸函数,即任取两点$x,y$,任取$\theta \in [0,1]$,必然有: $$\theta f(x) + (1-\theta) f(y) \geq f(\theta x + (1-\theta) y)$$
即:
$$\int_{0}^{1} f(x+\lambda(y-x)) d \lambda \leq \int_{0}^{1}(f(x)+\lambda(f(y)-f(x))) d \lambda=\frac{f(x)+f(y)}{2}$$
然后是充分性,即满足后式,必然能保证是凸函数,使用凸函数的第一定义证明: 任取两点$x,y$,任取$\theta \in [0,1]$,需要证明$\theta f(x) + (1-\theta) f(y) \geq f(\theta x + (1-\theta y))$
用反证法,也就是说函数不是凸函数,至少能找到一个$x, y \in dom f $和$\theta \in [0,1]$,使得 $$\theta f(x) + (1-\theta) f(y) < f(\theta x + (1-\theta) y)$$ 也就是说存在$x^*, y^*, \theta^*$关于$\theta$的函数: $$g(\theta) = f(\theta x + (1-\theta) y) - \theta f(x) - (1-\theta) f(y) >0$$
由于$\theta = 0$和$1$时上式均为0。所以一定在 $\theta^*$的左右存在两点$p,q$,使得$g(p) = 0, g(q) = 0, g(i)_{p \leq i \leq q} > 0$
取$x = p, y =q$,在原函数上有$\int_{0}^{1} f(p+\theta(p-q)) d \theta>\int_{0}^{1}(f(p)+\theta(f(p)-f(q))) d \theta=\frac{f(p)+f(q)}{2}$,与初始矛盾,所以反证法成立。
判断下列函数是否为凸函数、凹函数、拟凸函数与拟凹函数:
(a)$f(x) = e^x - 1, \textbf{dom}\ f = R$
(b)$f(x_1,x_2) = x_1 x_2, \textbf{dom}\ f = R_{++}^2$
(c)$f(x_1,x_2) = 1/(x_1 x_2), \textbf{dom}\ f = R_{++}^2$
(d)$f(x_1,x_2) = x_1 / x_2, \textbf{dom}\ f = R_{++}^2$
(e)$f(x_1,x_2) = x_1^2/ x_2, \textbf{dom}\ f = R \times R_{++}$
(f)$f(x_1,x_2) = x_1^{\alpha} x_2^{1-\alpha}, 0 \leq \alpha \leq 1, \textbf{dom}\ f = R_{++}^2$
(a) 由于原函数二阶可导 $f''(x) = e^x > 0$ 为凸函数,凸函数也一定是拟凸函数,同时还是拟凹函数
(b)
Hessain矩阵为:$$ \nabla^{2} f(x)=\left[\begin{array}{ll} 0 & 1 \newline 1 & 0 \end{array}\right] $$ 既非正定,又非负定,所以不是凸函数也不是凹函数。
$\alpha$-上水平集为凸集,是拟凹函数,下水平集不是凸集,所以不是拟凸函数
(c) Hessain矩阵为: $$ \nabla^{2} f(x)=\frac{1}{x_{1} x_{2}}\left[\begin{array}{cc} 2 /\left(x_{1}^{2}\right) & 1 /\left(x_{1} x_{2}\right) \newline 1 /\left(x_{1} x_{2}\right) & 2 / x_{2}^{2} \end{array}\right] \geq 0 $$ 是正定的,所以是凸函数,也是拟凸函数。不是凹函数,也不是拟凹函数。
(d) Hessain矩阵为: $$ \nabla^{2} f(x)=\left[\begin{array}{cc} 0 & -1 / x_{2}^{2} \newline -1 / x_{2}^{2} & 2 x_{1} / x_{2}^{3} \end{array}\right] $$ 既非正定,又非负定,所以不是凸函数也不是凹函数。 上水平集和下水平集均为半空间,所以既是拟凸的又是拟凹的。
(e) $$ \nabla^{2} f(x)=\left[\begin{array}{cc} 2 / x_{2} & -2 x_{1} / x_{2}^{2} \newline -2 x_{1} / x_{2}^{2} & 2 x_{1}^{2} / x_{2}^{3} \end{array}\right] \geq 0 $$ 是凸函数,也是拟凸函数,不是拟凹函数
(f) $$ \nabla^{2} f(x)=\left[\begin{array}{cc} \alpha(\alpha-1) x_{1}^{\alpha-2} x_{2}^{1-\alpha} & \alpha(1-\alpha) x_{1}^{\alpha-1} x_{2}^{-\alpha} \newline \alpha(1-\alpha) x_{1}^{\alpha-1} x_{2}^{-\alpha} & (1-\alpha)(-\alpha) x_{1}^{\alpha} x_{2}^{-\alpha-1} \end{array}\right] \leq 0 $$
是凹函数,也是拟凹函数。
函数的积或比,证明以下结论: $$\newline$$ (a)在某区间上的函数$f$和$g$都是凸函数,且都非减(或者都非增),二者都大于0,则函数$fg$在此区间上也是凸函数 $$\newline$$ (b)函数$f$和$g$都是凹函数,一个非减,一个非增,二者都大于0,则函数$fg$是凹函数 $$\newline$$ (c)函数$f$是凸函数,非减且大于0,$g$是凹函数,非增且大于0,那么函数$f/g$是凸函数
要证明$fg$的凹凸性,根据定义,则要证明: $$\theta f(x)g(x) + (1-\theta) f(y)g(y) 和 f(\theta x + (1-\theta)y)g(\theta x + (1-\theta)y) 的关系$$
要证明$f/g$的凹凸性,根据定义,则要证明: $$\theta f(x)/g(x) + (1-\theta) f(y)/g(y) 和 f(\theta x + (1-\theta)y)/g(\theta x + (1-\theta)y) 的关系$$
(a)
都凸,所以对于$x, y \in dom$, $\theta \in [0,1]$ $$\begin{array}{ll} f(\theta x + (1-\theta)y)g(\theta x + (1-\theta)y) &\leq (\theta f(x)+(1-\theta) f(y))(\theta g(x)+(1-\theta) g(y)) \newline & = \theta^2 f(x) g(x) + (1-\theta)^2 f(y) g(y) + \theta(1-\theta)(f(y)-f(x))(g(x)-g(y)) \end{array}$$
且非减且大于0,即$\theta(1-\theta)(f(y)-f(x))(g(x)-g(y)) \leq 0$,有: $$ \theta(1-\theta)(f(y)-f(x))(g(x)-g(y)) \leq 0 $$ 有 $$\theta f(x)g(x) + (1-\theta) f(y)g(y) \geq f(\theta x + (1-\theta)y)g(\theta x + (1-\theta)y)$$
即$fg$为凸函数
(b)
都凹,所以对于$x, y \in dom$, $\theta \in [0,1]$ $$\begin{array}{ll} f(\theta x + (1-\theta)y)g(\theta x + (1-\theta)y) &\geq (\theta f(x)+(1-\theta) f(y))(\theta g(x)+(1-\theta) g(y)) \newline & = \theta^2 f(x) g(x) + (1-\theta)^2 f(y) g(y) + \theta(1-\theta)(f(y)-f(x))(g(x)-g(y)) \end{array}$$
一个非减一个非增,有 $$ \theta(1-\theta)(f(y)-f(x))(g(x)-g(y)) \geq 0 $$ 有 $$\theta f(x)g(x) + (1-\theta) f(y)g(y) \leq f(\theta x + (1-\theta)y)g(\theta x + (1-\theta)y)$$
$fg$为凹函数
(c)
因为$f$为凸,非减且大于0,$g$为凹,非增且大于0,有 $$\begin{array}{ll} f(\theta x + (1-\theta)y)/g(\theta x + (1-\theta)y) &\leq (\theta f(x)+(1-\theta) f(y))/(\theta g(x)+(1-\theta) g(y)) \newline & \leq \theta f(x)/g(x) + (1-\theta) f(y)/g(y) \end{array}$$
有 $$\theta f(x)/g(x) + (1-\theta) f(y)/g(y) \geq f(\theta x + (1-\theta)y)/g(\theta x + (1-\theta)y)$$
$f/g$为凸函数
证明凸函数的二阶条件,也就是凸函数的充要条件是Hessian矩阵半正定
先证充分性,即凸函数可以推导出Hessain矩阵半正定:
根据凸函数的一阶定义 $$ f(y) \geq f(x) + \nabla f(x)(y-x) \newline f(x) \geq f(y) + \nabla f(y)(x-y) $$
有:
$$\nabla f(x) (y-x) \leq f(y) - f(x) \leq \nabla f(y)(y-x)$$
可得
$$\frac{\nabla f(y) - \nabla f(x)}{y-x} \geq 0$$
取$y \to x^+$,得:
$$\nabla^2 f(x) \geq 0$$
证明必要性,这里先考虑$n=1$的情况
取$x < y$,根据分部积分法,有:
$$ \begin{array}{ll} 0 & \leq \int_{x}^{y} f^{\prime \prime}(z)(y-z) dz \newline &= \left.\left(f^{\prime}(z)(y-z)\right)\right|_{z=x} ^{z=y} + \int_x^y f^{\prime}(z) dz \newline &=-f^{\prime}(x)(y-x)+f(y)-f(x), \end{array} $$
注: 第一个等号是分部积分法,即 $$f(x)g(x) = \int( f'(x)g(x) + f(x)g'(x)) \newline \int f'(x)g(x) = f(x)g(x) - \int f(x)g'(x) $$
有$$ f(y) \geq f(x) + f'(x)(y-x) $$ 通过一阶条件可知是凸函数
然后拓展到$n>1$的情况,根据凸函数的第二定义,如果$g(t) = f(x_0 + vt)$对于每个$x_0$和$v$而言都是凸函数的话,就可以得到$f(x)$是凸函数。
$g(t)$是凸函数也就是说它的二阶导大于等于0:
$$ g^{\prime \prime}(t)=v^{T} \nabla^{2} f\left(x_{0}+t v\right) v \geq 0 $$
因为有$\nabla^{2} f \geq 0$,所以上式成立,也就是说$f$是凸函数