信息论基础
信息是事物运动状态或存在方式的不确定性的描述
通信系统形式上传递的就是信息,需求来源于:
① 需要告知某信息给对方
② 需要接受某种信息。通信的结果就是消除不确定性或者获得信息。
信息论研究的目的在于:通过探索信息传输的规律,提高信息传输的有效性、可靠性和保密性,使得信息系统达到最优化。
数据:传送信息的实体
信号:数据的电气或电磁表现,数据在传输过程中的存在形式 (连续变化的称为模拟数据/信号,离散变化的数据称为数字数据/信号)
码元:用一个固定时长的信号波形代表一位k进制数字
信源:产生和发送数据的源头
信道:信号的传输媒介 s 信宿:接收数据的终点
速率:数据的传输速率,表示单位时间内传输的数据量,码元传输速率单位是波特(Baud),信息运输速率单位是 比特/秒 (b/s)
$$比特/秒 = 波特 \times \log_2电平数$$
波特:每秒内信息改变的次数,一波特就表示数字通道系统一秒钟传输一个码元
带宽:指信号具有的频带宽度,单位是赫兹(Hz),表示单位时间内从网络某一点到另一点所能通过的最高数据率,此时单位是bit/s
信息量
信息量 = 不确定性的减少量 = 收信前的不确定性 - 收信后的不确定性
某个事件发生的信息量是该事件发生的先验概率的函数:
$$I(a_i) = f[P(a_i)]$$
有$I(a_0 = 0) = \infty, I(a_0 = 1) = 0$
独立事件的联合信息量等于各自的信息量之和
自信息量的计算公式为:
$$ I(a_i) = \log \frac{1}{P(a_i)} $$
以2为底,单位为比特;以e为底,单位为奈特;以10为底,单位为哈特。
熵
反应了信源整体的不确定度
$$ H(x) = -\sum_x p(x)\log p(x) $$
联合熵: $$ H(X, Y) = -\sum_{x,y} p(x,y)\log p(x,y) $$
条件熵: $$ H(X | Y) = - \sum_y H(X|Y=y) p(y) = -\sum_{y} \sum_{x} p(x \mid y) p(y) \log p(x \mid y) $$
互信息: $$ I(X;Y) = \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)p(y)} $$
两个独立的随机变量的互信息等于0
信源编码与信道编码
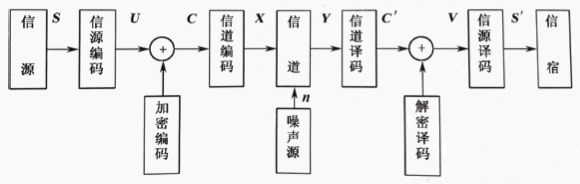
信号先经过信源编码,然后进入信道前经过信道编码。
信源编码的作用:信息量的压缩,减少原信号的冗余
信道编码的作用:信息量的增加,用于增加可靠性
带宽受限且有高斯白噪声干扰的信道的极限、无差错的信息传输速率
无线通信系统
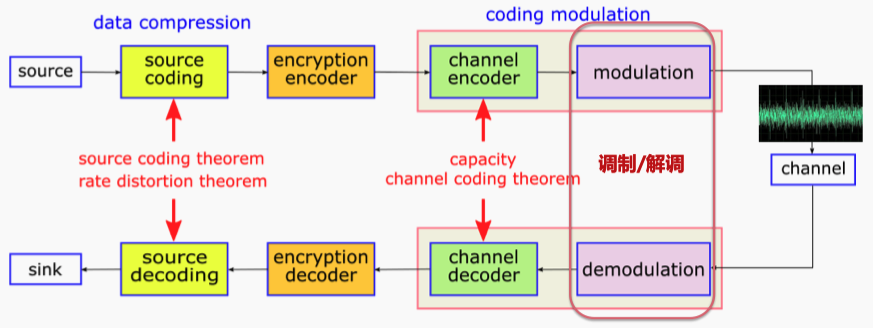
源信号依次经过信源编码、加密、信道编码、调制然后发送出去,接受时依次经过解调、信道解码、解密、信源解码然后接受。
调制
调制:将某个信息嵌入到另一个信号的过程,比如模拟信号通过采样、量化、数字化编码到数字信号的过程。
之所以要调制,是为了提高频率,从而让让信号客户要传播的更远,大气层对低频段的损耗非常高。
信源的信号有很多低频或者直流成分,很多信道不能直接传输。一方面需要调制成高频信号便于天线发射,一方面可以通过多路传输不同的基带信号,如果频率一样可能会干扰(广播的频率不一样就可以同时发射互不干扰)。
载波调制就是利用载波进行调制,把基带信号的频率搬移到较高的频段。
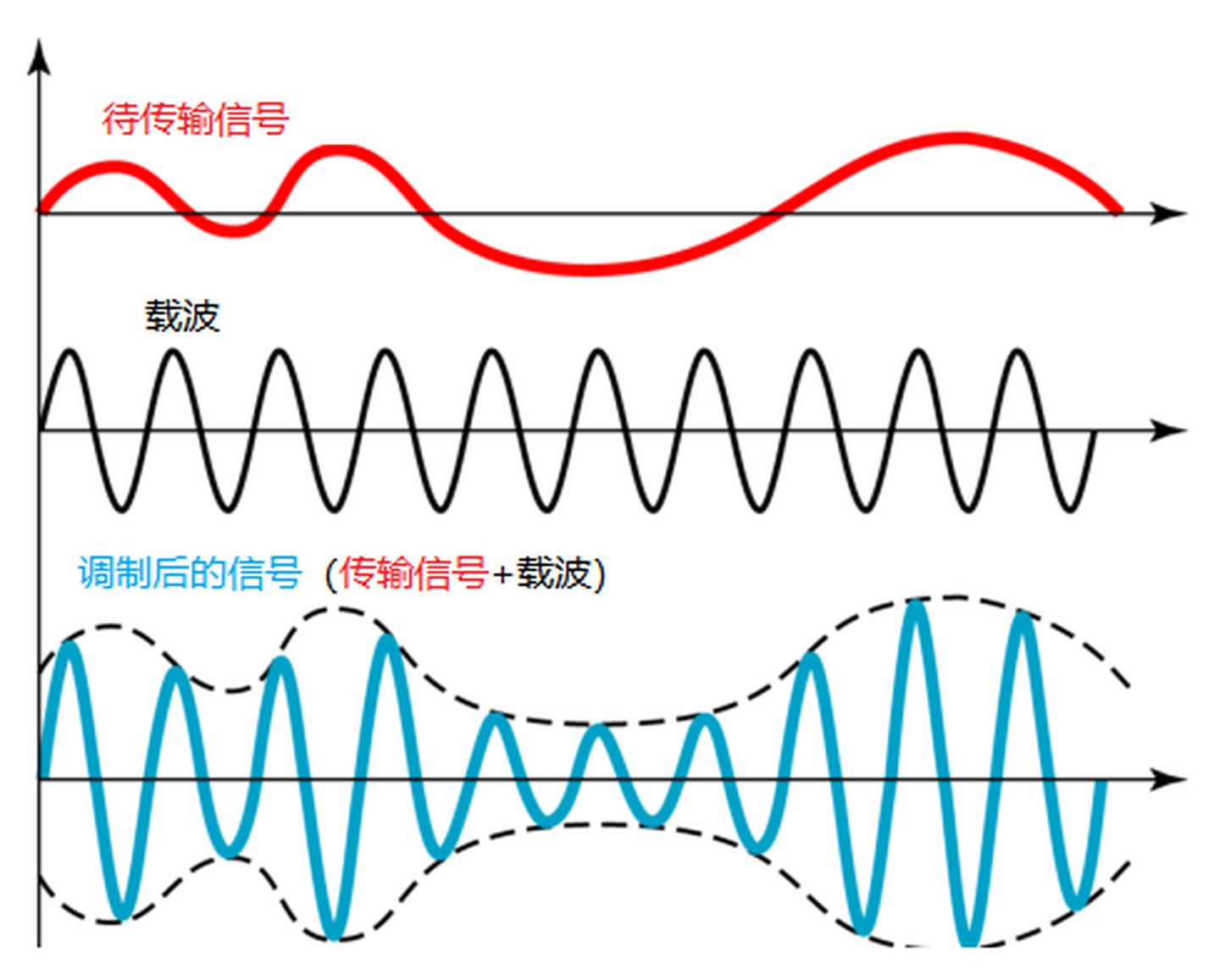
码元调制
码间串扰:在接收端收到的信号波形就失去了码元和符号之间的清晰的界限。
进行码元/符号调制的目的:用一个码元代表多个比特,在码元速率一定的情况下提高数据传输速率
Nyquist定理
在绝对理想的信道中,极限码元传输速率为$2W$ Baud
$W$是理想低通信道的带宽,单位为Hz $V$是每个码元离散电平的数目,$V$个电平就需要$log_2V$个二进制位
理想状态下的极限数据传输率 = $2Wlog_2V$ (单位 b/s)
超过这个界限就会出现严重的码间串扰
香农定理
信道的极限数据传输速率 = $Wlog_2(1+S/N)$
$S$是信道传输的平均功率 $N$为信道内部的高斯噪声功率
例子
- 带宽为6MHz,量化等级为4,无噪声,求最大传输速率
解:使用Nyquist定理,$C = 2 * W * log_2V = 2 * 6 * log_24 = 24Mbps$
- 带宽为3MHz,信噪比为20dB,二进制,求最大数据传输速率
解:使用香农定理
先化$S/N$的单位,$10lg(S/N) = 20 \to S/N = 100 $
$C= W * log_2{(1+S/N)} = 3 * log_2{(1+100)} \approx 20Kbps$
无线信道
传播的时候会遇到很多复杂的情况,造成信号的衰弱,根据信号传播的距离分为大尺度衰弱和小尺度衰弱。
大尺度衰弱
大尺度衰弱是发射和接受信号的距离较长,数百数千米
大尺度衰弱包括路径损耗和阴影效应:
路径损耗:随着路径长度的平方衰减,和方向等参数无关
阴影损耗:遇到障碍物时,后面的阴影区信号场比较弱,会造成损耗
小尺度衰弱
小尺度衰弱是数个或者数十个波长的距离
小尺度衰弱更为重要,其中造成小尺度衰弱的主要原因有多径效应和多普勒效应
包括频率选择性衰弱和时变特性
多径效应:由于电波传递的过程中有各种反射散射等,会导致到达时的信号是由多个状态叠加的,随机分布的幅度、相位、入角等合成之后使得接收到的信号删除衰弱和失真,比如极端情况刚好差半个波长然后刚好抵消(实际基本不可能,但是能说明其影响)
多普勒效应:是由于接收端和发射端之间的相对移动产生的
蜂窝网络
单基站覆盖:早期的移动通信是利用高塔上的天线大功率发射,但是业务通道很少
蜂窝通信网络:减少单个基站的发射功率,多小区覆盖,不同小区之间频率复用(频率复用是蜂窝移动通信的基石)
同频段小区之间可能会干扰,需要增加同频段小区之间的距离
不同簇之间使用相同频率的小区的最小距离$D$称为频率再用比例(就是两个相同频率的,看最接近的路径是多大)
小区切换,设定某个切换门限,低于门限值则进行切换,需要设定一个时间,持续低于这段时间再切换,从而避免乒乓球切换。
同频组网
单工:指的是只有一个方向的交互而没有反方向的交互 半双工:双方都可以发送信息,但是不能同时发送或者接受
半双工分为FDD(频分双工)和TDD(时分双工),FDD就是在不同的频率上同时发送,TDD用时间片轮转。
全双工:双方可以同时发送和接收消息
多址接入方式
复用:同样的频谱如何重复使用 多址:同样的频谱如何分给不同用户
多址其实就是要去找一种方式来分割为多个正交的数据流,从而将它们分开。
频分多址(FDMA):在频域复用多个数据流,用于多个用户 时分多址(TDMA):在时域复用多个数据流,用于多个用户 码分多址(CDMA):在码域复用多个数据流,用于多个用户 空分多址(SDMA):在空间上用于多个用户
把每个频谱比作一个房间,FDMA就是不同的用户去不同的方向聊天,TDMA就是依次排队去房间聊天,CDMA就是一窝蜂的一起说话,但是说的语言不同,只要认准自己的语言就能分开从而交流。
码片序列,将一个比特时间划分成m个短的间隔,称为码片。每个站被指派一个唯一的m bit码片序列,1则为自己的码片,0则发送自己的反码。
每个站分配的码片序列必须各不相同且相互正交
扩频技术,之前的一个bit变成了m个bit,发送的数据率是之前的m倍,宽度也提高到m倍
扩频通信采用直接序列扩频或者跳频扩频 直接序列扩频DSSS是通过比特率高很多的伪码序列对信号进行二次调频的技术
OFDM:正交频分复用,运行载波之间紧密相邻甚至部分重合,可以实现很高的频谱效率。通过IFFT,人为建立载波间正交性
OFDM发射机的两个核心模块:IFFT和加入循环前缀CP
MIMO与波束赋型
传输途径的分类
基站和终端的传输途径有SISO、MISO、SIMO、MIMO。
MISO是基站多个天线发出相同信号,在终端合成一路,是发送分集技术。
SIMO是一个天线通过两路路径发送信号,终端收到两个信号,数据也一样,是接受分集技术。 MIMO(Multiple Input Multiple Output,多进多出) 实现多路数据并行发送,获得空间复用增益。 实现多个字信号的有效合并,获得空间分集增益。
分集与复用
分集
分集就是把多个独立衰弱的副本提供给接收机,接受机将同一数据流的不同版本进行合并和恢复。减少深度衰弱的概率,从而提高性能。(提高鲁棒性)
分为空间分集(同一个信息从多根天线上发射出去)、时间分集(同一个信号以超过相干时间间隔重复发送)
频率分集就是在多个频域上对同一信号进行重复发送
分集又分为简单分集(完全相同)、编码分集(不同的版本)、选择分集(选择一个信道较好的天线发送)、波束分集等
空间分集的算法: 空时块码(STBC,Alamouti空时分组码),各个发射天线上的码字满足正交性。因为正交,所以接收端只需要简单处理。
接收机是2路发送信号与噪声的线性叠加
复用
空分复用就是在多条独立的路径上传输不同的数据,提高系统容量。(提高吞吐率) 高速流分为几个低速数据流分别进行编码和调制,然后在不同的天线发送,接收机将不同天线上接受到的数据流进行合并