算法笔记（二叉树篇）

理论

一些概念

满二叉树

如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

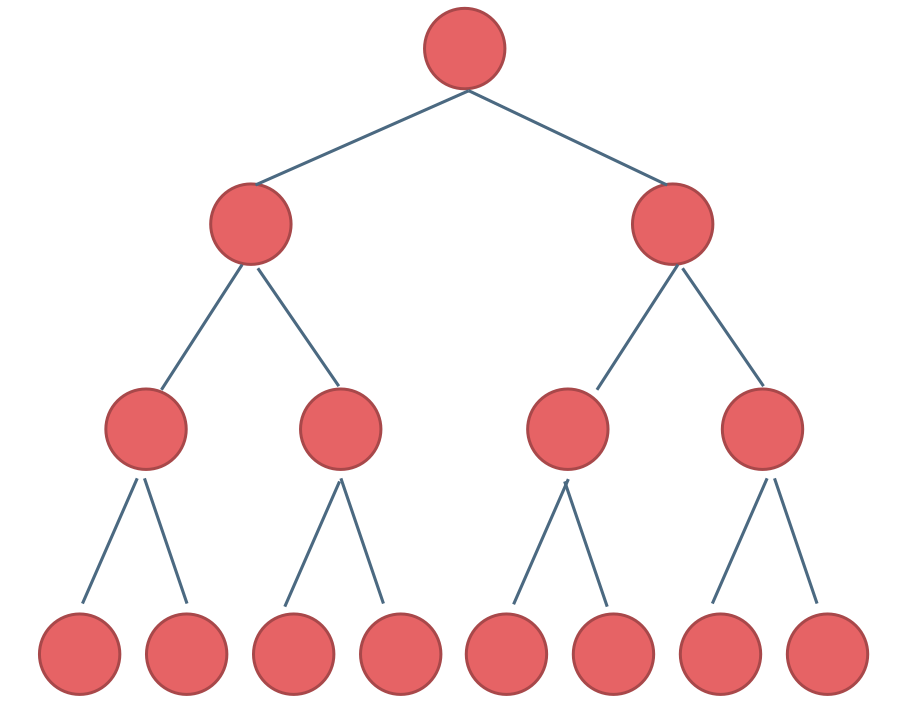
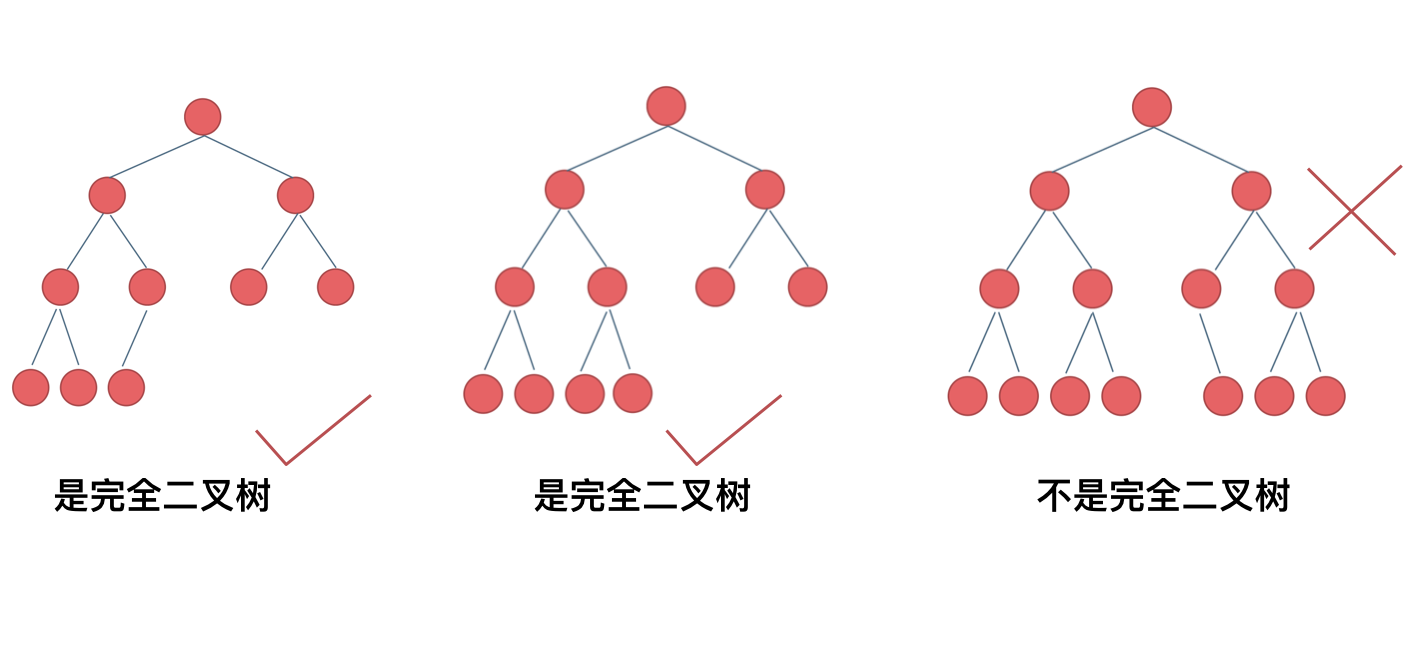
完全二叉树在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 $1$~$2^{h-1}$ 个节点。

二叉搜索树

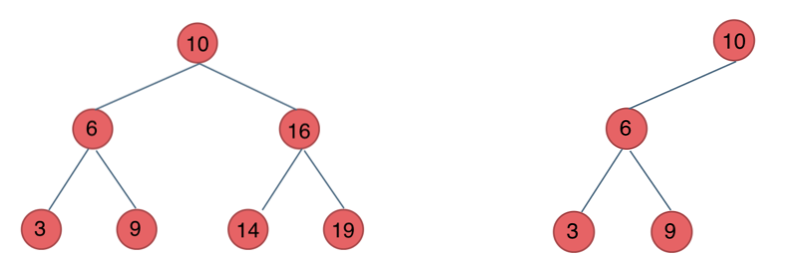
二叉搜索树是一棵有序树： ① 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； ② 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； ③ 它的左、右子树也分别为二叉排序树

平衡二叉搜索树（AVL树）

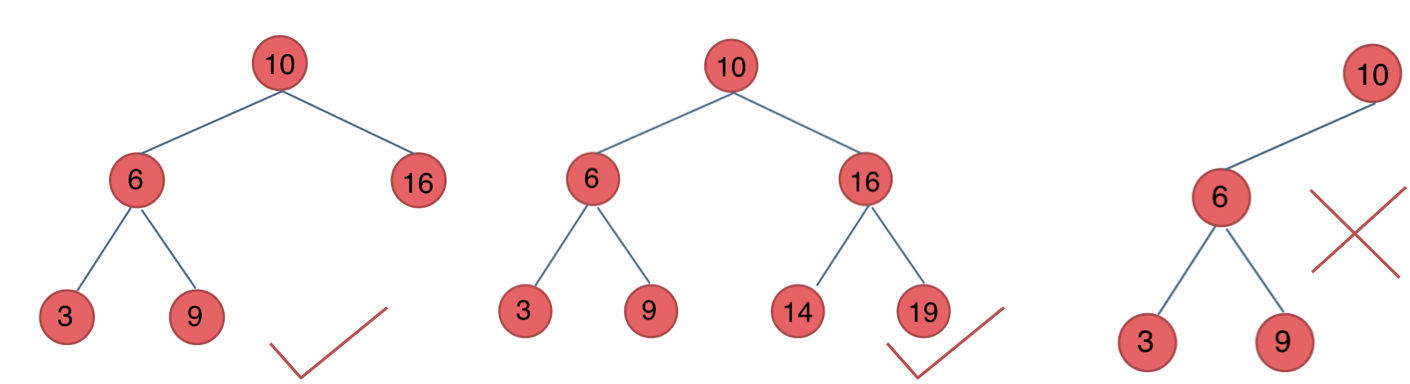
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

二叉树遍历

二叉树是递归最经典的应用，是回溯、动态规划、分治的基础。基本上递归问题也都可以抽象为二叉树的问题。比如快速排序可以抽象为二叉树的前序遍历，归并排序可以抽象为二叉树的后序遍历。

二叉树主要有两种遍历方式：

深度优先遍历：先往深走，遇到叶子节点再往回走。

前序遍历（递归法，迭代法）中序遍历（递归法，迭代法）后序遍历（递归法，迭代法）

广度优先遍历：一层一层的去遍历。

层次遍历（迭代法）

二叉树的递归遍历

写递归的思想在某些方面有点像数学归纳法，先假设一个方法能返回这个结果并相信这个方法，然后考虑最终的边界情况，之后将一个问题拆分为多个小的类似的问题递归解决。

写递归抓住三个要素：

确定递归函数的参数和返回值
确定终止条件
确定单层递归的逻辑

二叉树的迭代遍历

实际上递归的本质也是存在递归栈中，所以我们直接用栈就可以不需要递归，当然会比递归方法难写一些，用栈的迭代法可以节约空间降低复杂度。

二叉树层序遍历

二叉树的层次遍历也比较简单，需要利用队列这种数据结构。

代码框架如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


func levelOrder(root *TreeNode) [][]int {
  if root == nil {
    return [][]int{}
  }
  var queue []TreeNode
  queue = append(queue, *root)
  var result [][]int
  var row []int
  for len(queue) != 0 {
    length := len(queue)
    for i := 0; i < length; i++ {
      head := queue[0]
      if head.Left != nil {
        queue = append(queue, *head.Left)
      }
      if head.Right != nil {
        queue = append(queue, *head.Right)
      }
      row = append(row, head.Val)
      queue = queue[1:]
    }
    result = append(result, row)
    row = []int{}
  }
  return result
}

LeetCode 144. 二叉树的前序遍历 ☆

递归法：

二叉树遍历的递归法写起来都很简单

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


func preorderTraversal(root *TreeNode) []int {
  var result []int
  pTraversal(root, &result)
  return result
}

func pTraversal(cur *TreeNode, result *[]int) {
  if cur == nil {
    return
  }
  *result = append(*result, cur.Val)
  pTraversal(cur.Left, result)
  pTraversal(cur.Right, result)
}

迭代法，利用一个栈，注意是先放入右孩子再放入左孩子，这样出栈才是正确的顺序，前序遍历的迭代法也不难。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


func preorderTraversal(root *TreeNode) []int {
  var st []*TreeNode
  var result []int
  if root == nil {
    return result
  }
  st = append(st, root)
  for len(st) > 0 {
    cur := st[len(st)-1]
    result = append(result, cur.Val)
    st = st[:len(st)-1]
    if cur.Right != nil {
      st = append(st, cur.Right)
    }
    if cur.Left != nil {
      st = append(st, cur.Left)
    }
  }
  return result
}

LeetCode 145. 二叉树的后序遍历 ☆

迭代法

这里迭代和前序遍历很不一样，首先需要记录之前的节点是否被遍历过，可以采用一个map，key是TreeNode指针，value是是否被遍历的bool值，也可以采用一个符合结构来记录这个TreeNode是够被遍历：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


type MyTreeNode struct {
  Node    *TreeNode
  Visited bool
}

func postorderTraversal(root *TreeNode) []int {
  var st []*MyTreeNode
  var result []int
  if root == nil {
    return result
  }
  st = append(st, &MyTreeNode{Node: root, Visited: false})
  for len(st) > 0 {
    cur := st[len(st)-1]
    if cur.Visited || (cur.Node.Left == nil && cur.Node.Right == nil) {
      result = append(result, cur.Node.Val)
      st = st[:len(st)-1]
    } else {
      if cur.Node.Right != nil {
        st = append(st, &MyTreeNode{Node: cur.Node.Right, Visited: false})
      }
      if cur.Node.Left != nil {
        st = append(st, &MyTreeNode{Node: cur.Node.Left, Visited: false})
      }
      cur.Visited = true
    }
  }
  return result
}

LeetCode 94. 二叉树的中序遍历 ☆

递归法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


func inorderTraversal(root *TreeNode) []int {
  var result []int
  pTraversal(root, &result)
  return result
}

func pTraversal(cur *TreeNode, result *[]int) {
  if cur == nil {
    return
  }
  pTraversal(cur.Left, result)
  *result = append(*result, cur.Val)
  pTraversal(cur.Right, result)
}

迭代法

和后序遍历很像，也是要额外的空间来存储各个节点是否被访问，这里唯一不同的就是需要先把自己取出来，然后把右子节点放进去再把自己放进去，这个时候visited置为true，再把左子节点放进去

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


type MyTreeNode struct {
  Node    *TreeNode
  Visited bool
}

func inorderTraversal(root *TreeNode) []int {
  var st []*MyTreeNode
  var result []int
  if root == nil {
    return result
  }
  st = append(st, &MyTreeNode{Node: root, Visited: false})
  for len(st) > 0 {
    cur := st[len(st)-1]
    if cur.Visited || (cur.Node.Left == nil && cur.Node.Right == nil) {
      result = append(result, cur.Node.Val)
      st = st[:len(st)-1]
    } else {
      // 先把自己取出来
      st = st[:len(st)-1]
      if cur.Node.Right != nil {
        st = append(st, &MyTreeNode{Node: cur.Node.Right, Visited: false})
      }
      // 再把自己放回去
      st = append(st, &MyTreeNode{Node: cur.Node, Visited: true})
      if cur.Node.Left != nil {
        st = append(st, &MyTreeNode{Node: cur.Node.Left, Visited: false})
      }
    }
  }
  return result
}

LeetCode 226. 翻转二叉树 ☆

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


func invertTree(root *TreeNode) *TreeNode {
   // 边界情况
   if root == nil {
      return root
   }
   // 当前操作
   root.Left, root.Right = root.Right, root.Left
   // 递归
   invertTree(root.Left)
   invertTree(root.Right)
   return root
}

LeetCode 116. 填充每个节点的下一个右侧节点指针 ☆☆

最先想到的方法是建立一个队列，层序遍历，但是代码量会比较复杂，一个非常好的方法是递归，但是不能直接套：

1

connect(root.Left, root.Right)

这样的话比如上图的5和6就连不起来，所以应该多考虑一个节点，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


func connect(root *Node) *Node {
    if root == nil {
        return root
    }
    connectTwoNodes(root.Left, root.Right)
    return root
}

func connectTwoNodes(node1 *Node, node2 *Node) {
    if node1 == nil || node2 == nil {
        return
    }
    node1.Next = node2
    connectTwoNodes(node1.Left, node1.Right)
    connectTwoNodes(node1.Right, node2.Left)
    connectTwoNodes(node2.Left, node2.Right)
}

LeetCode 114. 二叉树展开为链表 ☆☆

首先相信flatten可以完成这个功能。然后分别套左右子树，然后root的Left断开，左子树的最后面接上右子树即可。当然因为这里要多一个左子树的循环走到底，浪费了时间，效率不高，但是容易理解。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


func flatten(root *TreeNode) {
    if root == nil {
        return
    }
    flatten(root.Left)
    flatten(root.Right)
    l := root.Left
    r := root.Right
    if l == nil {
        return
    }
    root.Left = nil
    root.Right = l
    for l.Right != nil {
        l = l.Right
    }
    l.Right = r
}

二叉搜索树

二叉搜索树（Binary Search Tree，BST）有着广泛的应用，通过BST可以高效的搜索元素。

BST的性质：

任意一个节点的左子树所有节点的值都小于该节点，右子树所有节点的值都大于该节点
任意一个节点的左右子树都是BST

搜索模板是：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


fun BSTSearch(TreeNode root, int target) {
    if (root.val == target)
        // 找到目标，做点什么
    if (root.val < target){
        BSTSearch(root.right, target)
    }
    if (root.val > target){
        BSTSearch(root.left, target)
    }
}

LeetCode 700. 二叉搜索树中的搜索 ☆

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


func searchBST(root *TreeNode, val int) *TreeNode {
    if root == nil {
        return nil
    }
    if root.Val == val {
        return root
    }
    if root.Val < val {
        return searchBST(root.Right, val)
    } else {
        return searchBST(root.Left, val)
    }
}

LeetCode 98. 验证二叉搜索树 ☆☆

二叉搜索树不能只看父节点和两个子节点的大小，而是整个左子树都小于，整个右子树都大于，所以单独开一个函数，多传入min和max两个参数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


func isValidBST(root *TreeNode) bool {
    return valid(root, nil, nil)
}

func valid(root *TreeNode, min *int, max *int) bool {
    if root == nil {
        return true
    }
    if (max != nil && root.Val >= *max) || (min != nil && root.Val <= *min) {
        return false
    }
    return valid(root.Left, min, &root.Val) && valid(root.Right, &root.Val, max)
}

LeetCode 701. 二叉搜索树中的插入操作 ☆☆

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


func insertIntoBST(root *TreeNode, val int) *TreeNode {
    if root == nil {
        root = &TreeNode{Val: val, Left: nil, Right: nil}
        return root
    }
    // 插入右子树
    if root.Val < val {
        root.Right = insertIntoBST(root.Right, val)
        return root
    } else {
        root.Left = insertIntoBST(root.Left, val)
        return root
    }
}

LeetCode 450. 删除二叉搜索树中的节点 ☆☆

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


func deleteNode(root *TreeNode, key int) *TreeNode {
    if root == nil {
        return nil
    }
    if root.Val == key {
        if root.Left == nil && root.Right == nil {
            return nil
        } else if root.Left == nil {
            root = root.Right
        } else if root.Right == nil {
            root = root.Left
        } else {
            // 获得左子树最大的节点
            leftMax := root.Left
            for leftMax.Right != nil {
                leftMax = leftMax.Right
            }
            root.Left = deleteNode(root.Left, leftMax.Val)
            leftMax.Left = root.Left
            leftMax.Right = root.Right
            root = leftMax
        }
    } else if root.Val > key {
        root.Left = deleteNode(root.Left, key)
    } else if root.Val < key {
        root.Right = deleteNode(root.Right, key)
    }
    return root
}

二叉搜索树的中序遍历就是有序数组

LeetCode 530.二叉搜索树的最小绝对差 ☆

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


func getMinimumDifference(root *TreeNode) int {
	minDelta := math.MaxInt
	traverse(root, &minDelta, &[]int{})
	return minDelta
}

func traverse(root *TreeNode, min *int, result *[]int) {
	if root == nil {
		return
	}
	traverse(root.Left, min, result)
	if len(*result) > 0 && root.Val-(*result)[len(*result)-1] < *min {
		*min = root.Val - (*result)[len(*result)-1]
	}
	*result = append(*result, root.Val)
	traverse(root.Right, min, result)
}

LeetCode 501. 二叉搜索树中的众数 ☆

加一个Prev指针，利用二叉搜索树的性质，一次遍历即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


func findMode(root *TreeNode) []int {
	var prev *TreeNode
	result := make([]int, 0)
	count, max := 1, 1
	var traverse func(node *TreeNode)
	traverse = func(node *TreeNode) {
		if node == nil {
			return
		}
		traverse(node.Left)
		if prev != nil && prev.Val == node.Val {
			count++
		} else {
			count = 1
		}
		if count >= max {
			if count > max && len(result) > 0 {
				result = []int{node.Val}
			} else {
				result = append(result, node.Val)
			}
			max = count
		}
		prev = node
		traverse(node.Right)
	}
	traverse(root)
	return result
}

二叉树较难想到的递归

LeetCode 236. 二叉树的最近公共祖先 ☆☆

本身代码量不多，但是思考稍微比较抽象。

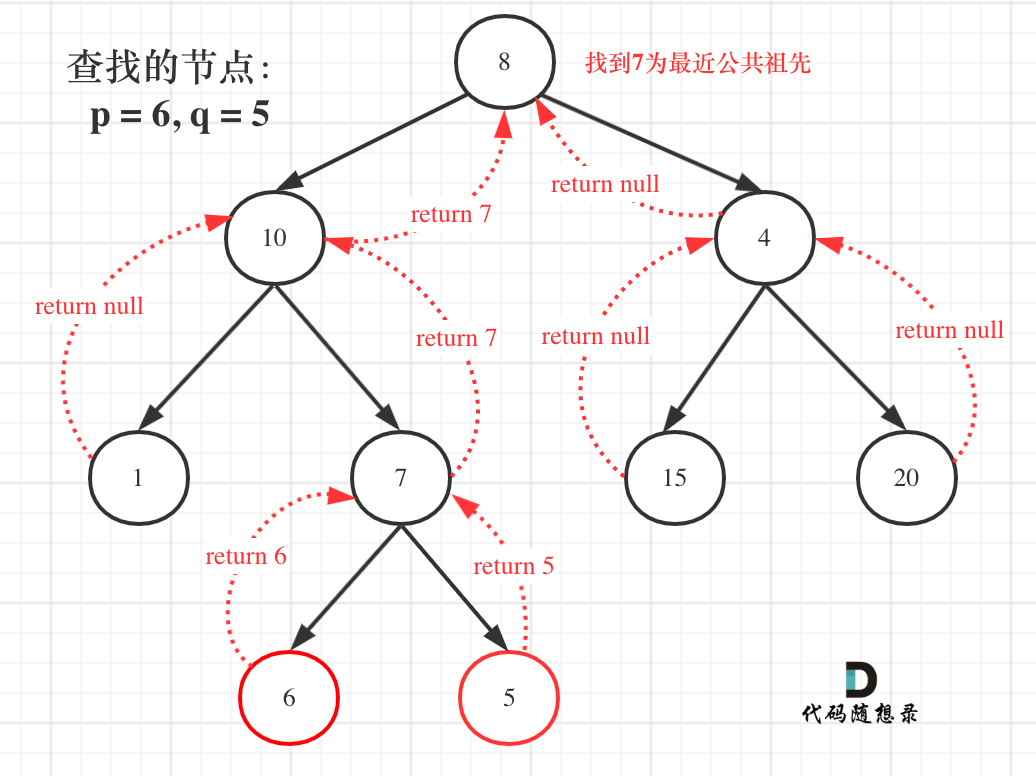
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
	if root == nil {
		return nil
	}
	// 如果遇到p或者q，就直接返回
	if root.Val == p.Val || root.Val == q.Val {
		return root
	}
	left := lowestCommonAncestor(root.Left, p, q)
	right := lowestCommonAncestor(root.Right, p, q)
	// 如果左右都不是nil，也就是说明当前节点左边找到了一个，右边找到了一个，返回当前节点
	if left != nil && right != nil {
		return root
	}
	// 如果左边返回的不是nil，但是右边是nil，说明要从左边找
	if left != nil {
		return left
	}
	return right
}

算法笔记（二叉树篇）

相关文章：