给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
1
2
3
4
5
6
7
8
9
10
|
func removeElement(nums []int, val int) int {
left := 0
for _, num := range nums {
if num != val {
nums[left] = num
left += 1
}
}
return left
}
|
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
思路:先找到最小的非负数的位置,然后左右双指针向左右移动,比较大小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
func sortedSquares(nums []int) []int {
var result []int
i, j := 0, 0
for _, num := range nums {
if num < 0 {
i += 1
} else {
break
}
}
j = i-1
for i < len(nums) || j >= 0 {
if i >= len(nums) {
result = append(result, nums[j]*nums[j])
j--
} else if j < 0 {
result = append(result, nums[i]*nums[i])
i++
} else {
if -nums[j] > nums[i] {
result = append(result, nums[i]*nums[i])
i++
} else {
result = append(result, nums[j]*nums[j])
j--
}
}
}
return result
}
|
掌握程度:基本掌握
二分查找本身原理比较简单,是一种分治的策略,但是实际写代码的时候,边界问题容易出错。
搜索有序数组中target的位置,没找到则返回-1
首先要明确的是搜索的边界范围,是[left, right]还是[left, right),比如下面两种都是对的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func search(nums []int, target int) int {
// 在[left, right]搜索
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else {
return mid
}
}
return -1
}
|
在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func searchInsert(nums []int, target int) int {
// 在[left, right]里寻找
left, right := 0, len(nums)-1
for left <= right {
mid := (right - left) >> 1 + left
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else {
return mid
}
}
return left
}
|
给定一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
func binarySearch(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := (right-left)>>1 + left
if nums[mid] == target {
return mid
} else if nums[mid] > target {
right = mid - 1
} else {
left = mid + 1
}
}
return -1
}
func searchRange(nums []int, target int) []int {
if len(nums) == 0 {
return []int{-1, -1}
}
findOne := binarySearch(nums, target)
if findOne == -1 {
return []int{-1, -1}
} else {
firstId, lastId := findOne, findOne
for firstId >= 0 && nums[firstId] == target {
firstId--
}
for lastId <= len(nums)-1 && nums[lastId] == target {
lastId++
}
return []int{firstId + 1, lastId - 1}
}
}
|
掌握程度:基本掌握
通过构造一个新的数组,存储前缀和,从而节约时间。这也是一个空间换时间的典型方法。
前缀和的代码框架为:
1
2
3
4
5
6
7
8
|
var preSumArray []int
preSum := 0
for _, i := range nums {
preSum += i
preSumArray = append(preSumArray, preSum)
}
区间[i,j]的累加量:preSumArray[j+1] - preSumArray[i]
|
设定一个辅助数组aux,第i个位置存的是原数组arr的0-i的和,然后计算原数组(i,j]之和时直接aux[j]-aux[i]即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
type NumArray struct {
Aux []int
}
func Constructor(nums []int) NumArray {
sum := 0
na := new(NumArray)
for _, v := range nums {
sum += v
na.Aux = append(na.Aux, sum)
}
return *na
}
func (this *NumArray) SumRange(left int, right int) int {
if left != 0 {
return this.Aux[right] - this.Aux[left-1]
} else {
return this.Aux[right]
}
}
|
无非是把一维数组换为了二维数组,需要求给定左上角点和右下角点围城矩形包含的元素和,方法还是一样的。
原矩阵matrix,创建一个二维辅助矩阵,其i行j列表示原矩阵左上角点和(i,j)点围成的矩形的和,原矩阵的任意一个矩形区域的和就可以通过四个矩形的容斥原理(左上+右下-右上-左下)算出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
type NumMatrix struct {
Matrix [][]int
}
func Constructor(matrix [][]int) NumMatrix {
var numMatrix NumMatrix
numMatrix.Matrix = make([][]int, len(matrix)+1)
for i := range numMatrix.Matrix {
numMatrix.Matrix[i] = make([]int, len(matrix[0])+1)
}
for i := 1; i <= len(matrix); i++ {
for j := 1; j <= len(matrix[i-1]); j++ {
numMatrix.Matrix[i][j] = numMatrix.Matrix[i-1][j] + numMatrix.Matrix[i][j-1] - numMatrix.Matrix[i-1][j-1] + matrix[i-1][j-1]
}
}
for i := 0; i <= len(matrix); i++ {
fmt.Println(numMatrix.Matrix[i])
}
for i := 0; i < len(matrix); i++ {
fmt.Println(matrix[i])
}
return numMatrix
}
func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
return this.Matrix[row2+1][col2+1] - this.Matrix[row1][col2+1] - this.Matrix[row2+1][col1] + this.Matrix[row1][col1]
}
|
这道题给出一个数组,要找出和为K的连续的子数组的个数,实际上很容易想到,先构造一个前缀和辅助数组,然后构造两个for循环找出每种可能的情况,但是这样效率很低:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func subarraySum(nums []int, k int) int {
var preSumArray []int
preSum := 0
resultSum := 0
for _, i := range nums {
preSum += i
preSumArray = append(preSumArray, preSum)
}
preSumArray = append([]int{0}, preSumArray...)
for i := 0; i < len(preSumArray); i++ {
for j := i + 1; j < len(preSumArray); j++ {
if preSumArray[j]-preSumArray[i] == k {
resultSum += 1
}
}
}
return resultSum
}
|
注意到,使用前缀和数组之后,这个问题就变成了从前缀和数组中,找两个数,其差为K,与2Sum问题类似,使用一个哈希表即可优化,只需要一次从小到大的遍历,存preSumArray[i]+K -> 次数的映射,如果新的preSumArray[j]在这个哈希表中,结果就加preSumArray[j]
所以优化为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func subarraySum(nums []int, k int) int {
var preSumArray []int
preSum := 0
resultSum := 0
for _, i := range nums {
preSum += i
preSumArray = append(preSumArray, preSum)
}
preSumArray = append([]int{0}, preSumArray...)
auxMap := make(map[int] int)
for i := 0; i < len(preSumArray); i++ {
if _, ok := auxMap[preSumArray[i]]; ok{
resultSum += auxMap[preSumArray[i]]
}
auxMap[preSumArray[i]+k] += 1
}
return resultSum
}
|
差分相当于前缀和的逆变换,数组前缀和的差分就是原数组。差分数组的适用场景是频繁对区间内的元素进行增减运算。
差分数组diff[i] = arr[i] - arr[i-1]
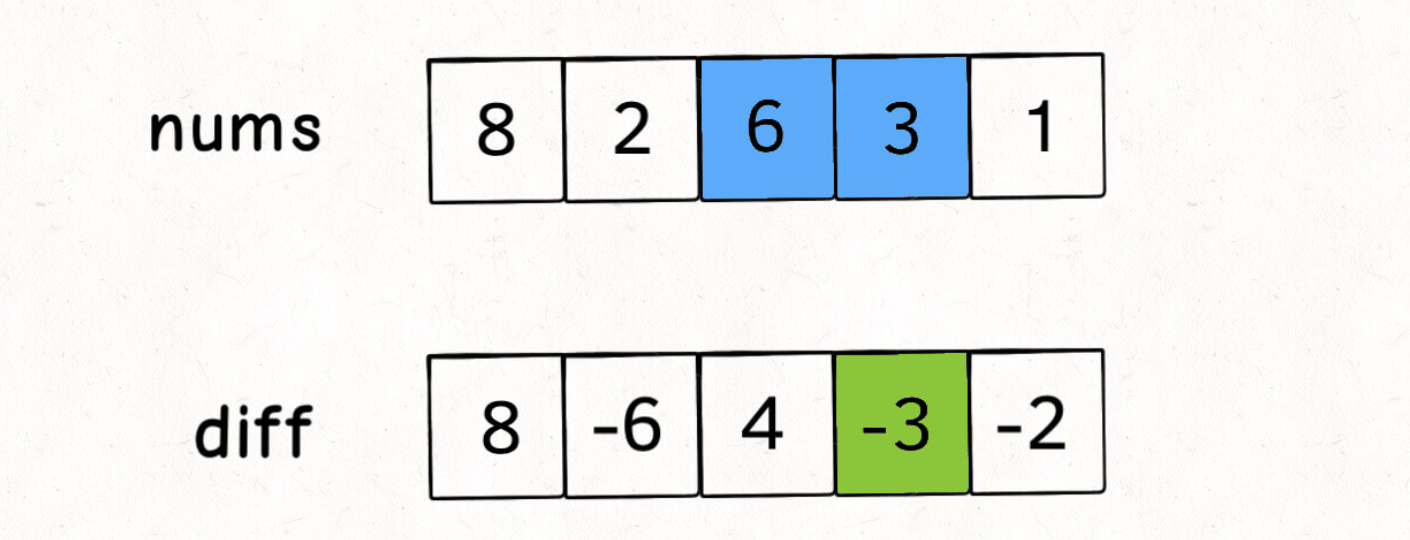
很容易发现差分数组做一次前缀和,就可以恢复为原数组。
此时如要要对原数组区间[i,j]统一增加k,那么只需要差分数组diff[i] += k,diff[j+1] -= k即可。
差分数组的代码框架为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
var diffArray []int{nums[0]}
for _, i := range nums {
diffArray = append(diffArray, nums[i] - nums[i-1])
}
// 区间[i, j]上增加val
diff[i] += val
if j + 1 < len(diff){
diff[j+1] -= val
}
// 构造前缀和还原
var result []int
preSum := 0
for _, i := range diffArray {
preSum += i
result = append(result, preSum)
}
|
直接考察差分数组,直接套代码框架即可。(不过该题为LeetCode会员题)
题目例子如下:
输入:bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出:[10,55,45,25,25]
解释:
航班编号 1 2 3 4 5
预订记录 1 : 10 10
预订记录 2 : 20 20
预订记录 3 : 25 25 25 25
总座位数: 10 55 45 25 25
answer = [10,55,45,25,25]
实际上还是区间加法,只是加了一个应用场景。
不过这里注意航班从1开始,所以first和last先-1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
func corpFlightBookings(bookings [][]int, n int) []int {
result := make([]int, n)
diffArray := make([]int, n)
for _, booking := range bookings{
first := booking[0]
last := booking[1]
seats := booking[2]
diffArray[first-1] += seats
if last < n{
diffArray[last] -= seats
}
}
cur := 0
for i, diff := range diffArray{
cur += diff
result[i] = cur
}
return result
}
|
乘客行程计划表trips[][],其中 trips[i] = [num_passengers, start_location, end_location]
车子的容量是capacity,问中途是否可能接完所有乘客。
本质上还是和上面一样,不同的是注意可以先下后上,diffArray的生成方式要看具体的问题,最后转换为前缀和,看当前的载客量是否都小于capacity:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
func carPooling(trips [][]int, capacity int) bool {
maxLength := 0
for _, trip := range trips{
if trip[2] > maxLength{
maxLength = trip[2]
}
}
diffArray := make([]int, maxLength+1)
for _, trip := range trips{
numP := trip[0]
from := trip[1]
to := trip[2]
diffArray[from] += numP
diffArray[to] -= numP
}
cur := 0
for _, i := range diffArray{
cur += i
if cur > capacity{
return false
}
}
return true
}
|
很简单,比如原地旋转图像,顺时针旋转90°等于先沿着对角线转置,再对于每一行进行翻转。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func rotate(matrix [][]int) {
n := len(matrix)
// 先转置
for i, _ := range matrix {
for j := i + 1; j < n; j++ {
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
}
}
// 对于每行,左右颠倒
for i, _ := range matrix {
for j := 0; j < n/2; j++ {
matrix[i][j], matrix[i][n-1-j] = matrix[i][n-1-j], matrix[i][j]
}
}
}
|
按照顺时针螺旋遍历返回矩阵的所有元素

用四元组确定一个矩形,这个矩形随着每次遍历都有改变。这里用左上角的坐标和width、height确定。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
func spiralOrder(matrix [][]int) []int {
var arr []int
x, y, width, height := 0, 0, len(matrix[0]), len(matrix)
for width > 0 && height > 0 {
if height > 0 {
for i := x; i < x+width; i++ {
arr = append(arr, matrix[y][i])
}
height -= 1
y += 1
}
if width > 0 {
for i := y; i < y+height; i++ {
arr = append(arr, matrix[i][x+width-1])
}
width -= 1
}
if height > 0 {
for i := x + width - 1; i >= x; i-- {
arr = append(arr, matrix[y+height-1][i])
}
height -= 1
}
if width > 0 {
for i := y + height - 1; i >= y; i-- {
arr = append(arr, matrix[i][x])
}
width -= 1
x += 1
}
}
return arr
}
|
和前一题相反,给定一个n,返回一个顺时针螺旋排列的正形矩阵。
代码只需要微调即可:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
func generateMatrix(n int) [][]int {
matrix := make([][]int, n)
for i := range matrix{
matrix[i] = make([]int, n)
}
x, y, width, height := 0, 0, n, n
num := 1
for width > 0 && height > 0 {
if height > 0 {
for i := x; i < x+width; i++ {
matrix[y][i] = num
num += 1
}
height -= 1
y += 1
}
if width > 0 {
for i := y; i < y+height; i++ {
matrix[i][x+width-1] = num
num += 1
}
width -= 1
}
if height > 0 {
for i := x + width - 1; i >= x; i-- {
matrix[y+height-1][i] = num
num += 1
}
height -= 1
}
if width > 0 {
for i := y + height - 1; i >= y; i-- {
matrix[i][x] = num
num += 1
}
width -= 1
x += 1
}
}
fmt.Println(matrix)
return matrix
}
|

